CÓDIGOS DE TRANSMISIÓN Y DETECCIÓN DE ERRORES

Modos de Transmisión

Esencialmente, hay cuatro modos de transmisión para los circuitos de comunicación de datos: simples, half duplex, full y full duplex.

Simplex.- Con la operación simplex, la transmisión de datos no se puede dirigir; la información se puede enviar sólo en una dirección. Las líneas simples, también se llaman líneas sólo para recibir, sólo para transmitir o de un solo sentido. La televisión comercial y sistemas de radio son ejemplos de transmisión simples.

Half duplex (HDX).- En el modo half duplex, la transmisión de datos es posible en ambas direcciones, pero no al mismo tiempo. Las líneas half duplex también se llaman de dos sentidos alternados o líneas de cualquier sentido. La banda civil (CB), es un ejemplo de transmisión half duplex.

Full Duplex (FDX).- En el modo de full duplex las transmisiones son posibles en ambas direcciones simultáneamente, pero deben estar las mismas dos estaciones. Las líneas de full duplex, también se llaman de dos sentidos simultáneas, duplex o líneas de dos sentidos. Un sistema telefónico estándar es un ejemplo de la transmisión de full duplex.

Full/ full duplex (F/FDX).- En el modo F/FDX, la transmisión es posible en ambas direcciones al mismo tiempo, pero no entre las mismas dos estaciones (es decir, una estación está transmitiendo a una segunda estación y recibiendo de una tercera estación, al mismo tiempo). F/FDX es posible sólo en los circuitos de multipunto. El sistema postal de EUA, es un ejemplo de una transmisión full/full duplex.

Operación de dos hilos contra cuatro hilos.

Dos hilos, como el nombre lo indica, envuelve un medio de transmisión que utiliza dos líneas de cable (una señal y una de referencia) o una configuración que es equivalente a tener sólo dos líneas de cable. Con la operación a dos hilos, es posible la transmisión simplex, half duplex o full duplex. Para la operación full duplex, las señales se propagan en direcciones opuestas, deben ocupar diferentes anchos de banda; de otra manera, se mezclarán en forma lineal y tendrán interferencia una con otra. Cuatro hilos, como el nombre lo indica, involucra un medio de transmisión que usa cuatro cables (dos se usan para las señales que se están propagando en direcciones opuestas y dos se usan como referencia) o una configuración que es equivalente a tener cuatro cables. Con la operación a cuatro hilos las señales se propagan en direcciones opuestas, están físicamente separadas y, por lo tanto, pueden ocupar los mismos anchos de banda sin interferir una con otra. La operación a cuatro hilos proporciona más aislamiento y se prefiere sobre la de dos hilos, aunque la de cuatro hilos requiere el doble de cables y, consecuentemente, el costo es doble.

Un transmisor y su receptor asociado son equivalentes a un circuito de dos hilos.

Un transmisor y un receptor para ambas direcciones de propagación es equivalente a un circuito a cuatro hilos. Con la transmisión y full duplex sobre una línea de dos hilos, el ancho de banda disponible debe dividirse a la mitad del valor del half duplex. Consecuentemente, la operación de full duplex sobre dos hilos requiere el doble del tiempo para transferir la misma cantidad de información.

Códigos de Comunicación de Datos.

Los códigos de comunicación de datos son secuencias de bit prescritas, usadas para codificar caracteres y símbolos. Consecuentemente, los códigos de comunicación de datos frecuentemente se llaman conjuntos de caracteres, códigos de caracteres, códigos de símbolo, o lenguaje de caracteres. Esencialmente, existen sólo tres tipos de caracteres usados en los códigos de comunicación de datos: caracteres de control de enlace de datos, los cuales se usan para facilitar el flujo ordenado de información, de una fuente a un destino; caracteres de control gráfico, lo cual involucra la síntesis o presentación de la información en la terminal de recepción, y caracteres alfa/numéricos, los cuales se usan para representar los múltiples símbolos usados para letras, números y puntuación en el lenguaje inglés.

El primer código de comunicaciones de datos, que tuvo un uso amplio, fue el código Morse. El código Morse usaba tres símbolos de longitud desigual (punto, guión y espacio), para codificar caracteres alfa/numéricos, signos de puntuación y una palabra de interrogación.

El código Morse es inadecuado, para usar en equipos de computadoras digitales modernas, porque todos los caracteres no tienen el mismo número de símbolos o requerimientos de la misma cantidad de tiempo en ser enviados y cada operador del código Morse transmite el código a una velocidad diferente. Además, con el código Morse, hay una selección insuficiente de caracteres de control gráficos y de enlace de control para facilitar la transmisión y presentación de los dats normalmente usados en las aplicaciones de computadora contemporáneas.

Los tres conjuntos de caracteres, más comunes, actualmente usados para la codificación de caracteres son: el código Buadot, el código Estándar Americano para el Intercambio de Información (ASCII) y el código de Intercambio de Decimal Codificado en Binario Extendido (EBCDIC).

Código Baudot (a veces llamado código Telex ).- Fue el primer código de caracteres de tamaño fijo. El código Baudot fue desarrollado por un ingeniero postal francés, Thomas Murray, en 1875 y nombrado después Emilie Baudot, un pionero en la impresión telegráfica. El código Baudot es un código de caracteres de 5 bits que se usa principalmente para equipo de teletipo de baja velocidad, tal como el sistema TWX/Telex . Con el código de 5 bits existen sólo 25 o 32 combinaciones posibles, lo cual es insuficiente para representar las 26 letras del alfabeto, los 10 dígitos y los diversos signos de puntuación, así como caracteres de control. Por lo tanto, el código Baudot usa caracteres de cambio de posición de letra, para expandir su capacidad a 58 caracteres. La última versión del código Baudot está recomendada por la CCITT como el Alfabeto Internacional No. 2 . El código Baudot, aún lo usa la Western Union Company para el TWX y los sistemas de teletipo Telex . Los servicios de noticias, AP y UPI, por muchos años usaron el código Baudot para enviar la información de noticias a todo el mundo. La versión más reciente del código Baudot se muestra en la siguiente tabla.

Código Baudot

Desplazamiento de
Carácter		Código Binario
Letra	Figura	Bit	4	3	2	1	0
A	-		1	1	0	0	0
B	?		1	0	0	1	1
C	:		0	1	1	1	0
D	$		1	0	0	1	0
E	3		1	0	0	0	0
F	!		1	0	1	1	0
G	&		0	1	0	1	1
H	#		0	0	1	0	1
I	8		0	1	1	0	0
J	‘		1	1	0	1	0
K	(		1	1	1	1	0
L	)		0	1	0	0	1
M	.		0	0	1	1	1
N	,		0	0	1	1	0
O	9		0	0	0	1	1
P	0		0	1	1	0	1
Q	1		1	1	1	0	1
R	4		0	1	0	1	0
S	bel		1	0	1	0	0
T	5		0	0	0	0	1
U	7		1	1	1	0	0
V	;		0	1	1	1	1
W	2		1	1	0	0	1
X	/		1	0	1	1	1
Y	6		1	0	1	0	1
Z	“		1	0	0	0	1
Desplazamiento de la figura			1	1	1	1	1
Desplazamiento de la letra			1	1	0	1	1
Espacio			0	0	1	0	0
Alimentación de línea (LF)			0	1	0	0	0
Blanco (nulo)			0	0	0	0	0

Código ASCII.- En 1963, en un esfuerzo por estandarizar los códigos de comunicaciones de datos, Estados Unidos adoptó el código de teletipo modelo 33, del Sistema Bell, como el Código de Información Estándar de Estados Unidos de América (USAASCII), mejor conocido, simplemente como ASCII-63. Desde su adopción, ASCII ha progresado genéricamente por las versiones de 1965, 1967 y 1977, con la versión de 1977 recomendada por la CCITT como el Alfabeto Internacional No.5. ASCII es un conjunto de caracteres de 7 bits que tiene 2 EXP 7 o 128 combinaciones. Con ASCII, el bit menos significativo (LSB) se designa como b(0) y el bit más significativo (MSB) se designa como b(6). El b(7) no es parte del código ASCII, pero generalmente se reserva para el bit de paridad. En realidad, con cualquier conjunto de caracteres, todos los bits son igualmente importantes, porque el código no representa un número binario con más peso. Es común con los códigos de caracteres referirse a bits por su orden; b(0) es el bit orden cero, b(1) es el bit de primer orden, etcétera. Con la transmisión serial, el bit transmitido primero se llama LSB. Con ASCII, el bit de orden bajo b(0), es el LSB y se transmite primero. El ASCII es probablemente el código más frecuentemente usado hoy en día. La versión de 1977 del código ASCII se muestra en la siguiente tabla.

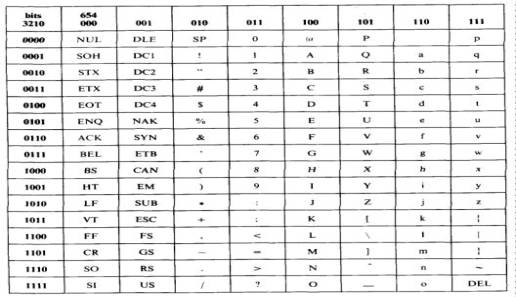
Código ASCII

Todas sus posibilidades son usadas, dividiéndose en: caracteres de control, caracteres especiales, letras mayúsculas, letras minúsculas, números.

NRZ(Non Return to Zero).- No Retorno a cero, utiliza un nivel diferente de tensión para cada uno de los dos dígitos binarios. Tiene la propiedad de que el nivel de tensión se mantiene constante durante la duración del BIT; es decir, no hay transiciones (no hay retorno al nivel cero de tensión). Por ejemplo, la ausencia de tensión se puede usar para representar un 0 binario, mientras que un nivel constante y positivo de tensión puede representar al 1. Aunque es mas común usar un nivel negativo para representar un valor binario y una tensión positiva para representar al otro. Es el esquema más sencillo ya que se codifica un nivel de tensión como un 1 y una ausencia de tensión como un 0 ( o al revés ) .

Ventajas : sencillez , fácil de implementar , uso eficaz del ancho de banda .

Desventajas : presencia de componente en continua , ausencia de capacidad de sincronización. Se suelen utilizar en grabaciones magnéticas .

Otra modalidad de este tipo de codificación es la NRZI que consiste en codificar los bits cuando se producen cambios de tensión ( sabiendo la duración de un BIT , si hay un cambio de tensión , esto se codifica por ejemplo como 1 y si no hay cambio , se codifica como 0 ) . A esto se le llama codificación diferencial . Lo que se hace es comparar la polaridad de los elementos de señal adyacentes , y esto hace posible detectar mejor la presencia de ruido y es más difícil perder la polaridad de una señal cuando hay dificultades de transmisión .

NRZ-L (No Return to Zero - Level).- Nivel no retorno a cero se usa generalmente para generar o interpretar los datos binarios en las terminales y otros dispositivos.

NRZI (No Return to Zero, invert on ones).- Al igual que NRZ-L, mantiene constante el nivel de tensión durante la duración de un BIT. Los datos se codifican mediante la presencia o ausencia de una transición de la señal al principio del intervalo de duración del BIT. Un1 se codifica mediante la transición (bajo a alto o alto a bajo) al principio del intervalo de señalización, mientras que un 0 se representa por la ausencia de transición. NRZI es un ejemplo de codificación diferencial, en la cual la codificación de cada BIT se hace de la siguiente manera: si se trata del valor binario 0, se codifica con la misma señal que el BIT anterior, si se trata de un valor binario 1, entonces se codifica con una señal diferente que la utilizada para el BIT precedente. Una ventaja es que en un sistema complicado de transmisión, no es difícil perder la polaridad de la señal. Por ejemplo, en una línea de par trenzado, si los cables se invierten accidentalmente, todos los 1y 0 en el NRZ - L se invitarán. Esto no pasa en un esquema diferencial.

Los códigos NRZ son los más fáciles de implementar y además se caracterizan por hacer un uso eficaz del ancho de banda.

Manchester .- En la codificación Manchester, cada período de un BIT se divide en dos intervalos iguales. Un BIT binario de valor 1 se transmite con valor de tensión alto en el primer intervalo y un valor bajo en el segundo. Un BIT 0 se envía al contrario, es decir, una tensión baja seguida de un nivel de tensión alto. Este esquema asegura que todos los bits presentan una transición en la parte media, proporcionando así un excelente sincronismo entre el receptor y el transmisor. Una desventaja de este tipo de transmisión es que se necesita el doble del ancho de banda para la misma información que el método convencional.

Manchester Diferencial.- Combinación de sincronización y datos. Este mecanismo de señalización binaria combina datos y pulsos de sincronización en “símbolos de bits”. Cada símbolos de BIT es separado en dos mitades, conteniendo la segunda mitad el inverso binario de la primera mitad. Siempre tiene lugar una transición en medio de cada símbolo de BIT. Se codifica un “espacio” como una repetición del símbolo de BIT anterior, generando de ese modo una transición tanto al comienzo como en el medio del símbolo de BIT. Se codifica una “marca” como el inverso del símbolo de BIT anterior, generando de ese modo una transición sólo en el medio. La codificación diferencial Manchester es una variación puesto que en ella, un bit de valor 1 se indica por la ausencia de transición al inicio del intervalo, mientras que un bit 0 se indica por la presencia de una transición en el inicio, existiendo siempre una transición en el centro del intervalo. El esquema diferencial requiere un equipo más sofisticado, pero ofrece una mayor inmunidad al ruido. El Manchester Diferencial tiene como ventajas adicionales las derivadas de la utilización de una aproximación diferencial.

Todas las técnicas bifase fuerzan al menos una transición por cada BIT pudiendo tener hasta dos en ese mismos periodo. Por tanto, la máxima velocidad de modulación es el doble que en los NRZ, esto significa que el ancho de banda necesario es mayor. No obstante, los  esquemas bifase tienen varias ventajas:

Definición de los formatos de codificación digital de señales

No retorno a cero (NRZ-L)

0 = nivel alto

1 = nivel bajo

No retorno a cero invertido (NRZI)

0 = no hay transición al comienzo del intervalo (un bit cada vez)

1 = transición al comienzo del intervalo

Bipolar AMI

0 = no hay señal

1 = nivel positivo o negativo alternante

Manchester

0 = transición de alto a bajo en mitad del intervalo

1 = transición de bajo a alto en mitad del intervalo

Manchester Diferencial

Siempre hay una transición en mitad del intervalo

0 = transición al principio del intervalo

1 = no hay transición al principio del intervalo

Caracteres de Control

Código EBCDIC.- EBCDIC es un código de caracteres de 8 bits, desarrollado por IBM y se usa, extensamente, en IBM y equipo compatible con IBM. Con 8 bits, son posibles 2 EXP 8 o 256 combinaciones, haciendo que EBCDIC sea el conjunto de caracteres más poderoso. Observe que con EBCDIC el LSB se designa como b(7) y el MSB se designa como b(0). Por lo tanto, transmite al final. El código EBCDIC no facilita el uso de bit de paridad. El código EBCDIC se muestra en la siguiente tabla.

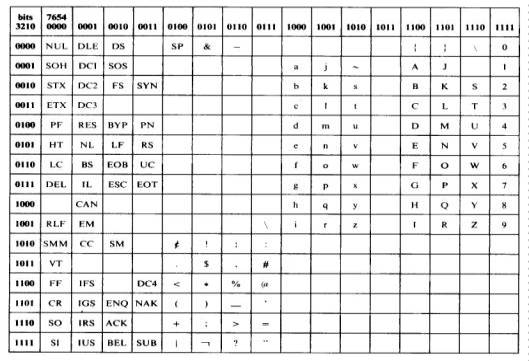
Código EBCDIC

Letras mayúsculas de la A a la Z: se dividen en tres grupos (A-I), (J-R), (S-Z) y en las primeras cuatro posiciones se identifica el grupo al cual pertenece la letra y en las restantes cuatro posiciones el dígito correspondiente a la posición de la letra en el grupo.

La letra Ñ se representa 0 1 1 0 1 0 0 1

Los dígitos del cero (0) al nueve (9): se identifican con un uno en las primeras cuatro posiciones y en las restantes cuatro posiciones el dígito en binario.

Datos y señales digitales

Una señal es digital si consiste en una serie de pulsos de tensión . Para datos digitales no hay más que codificar cada pulso como BIT de datos .

En una señal unipolar ( tensión siempre del mismo signo ) habrá que codificar un 0 como una tensión baja y un 1 como una tensión alta ( o al revés ) .

En una señal bipolar ( positiva y negativa ) , se codifica un 1 como una tensión positiva y un 0 como negativa ( o al revés ) .

La razón de datos de una señal es la velocidad de transmisión expresada en bits por segundo , a la que se transmiten los datos .

La razón de modulación es la velocidad con la que cambia el nivel de la señal , y depende del esquema de codificación elegido .

Un aumento de la razón de datos aumentará la razón la tasa de error por BIT.

Un aumento del ancho de banda permite un aumento en la razón de datos de error por BIT.

Un aumento de la relación señal-ruido ( S/N ) reduce Para mejorar las prestaciones del sistema de transmisión , se debe utilizar un buen esquema de codificación , que establece una correspondencia entre los bits de los datos y los elementos de señal .

Factores a tener en cuenta para utilizar un buen sistema de codificación :

1. Espectro de la señal : La ausencia de componentes de altas frecuencias , disminuye el ancho de banda . La presencia de componente continua en la señal obliga a mantener una conexión física directa ( propensa a algunas interferencias ) . Se debe concentrar la energía de la señal en el centro de la banda para que las interferencias sean las menores posibles .

2. Sincronización : para separar un bit de otro , se puede utilizar una señal separada de reloj ( lo cuál es muy costoso y lento ) o bien que la propia señal porte la sincronización , lo cuál implica un sistema de codificación adecuado .

3. Detección de errores : es necesaria la detección de errores ya en la capa física .

4. Inmunidad al ruido e interferencias : hay códigos más robustos al ruido que otros .

5. Coste y complejidad : el coste aumenta con el aumento de la razón de elementos de señal .

Códigos de corrección de errores.

Los diseñadores de redes han desarrollado dos estrategias básicas para manejar los errores. Una es incluir suficiente información redundante en cada bloque de datos transmitido para que el receptor pueda deducir lo que debió sel el carácter transmitido. La otra estratégia es incluir sólo suficiente redundancia para que el receptor sepa que ha ocurrido un error (pero no qué error) y entonces solicite una retransmisión. La primera estrategia usa códigos de corrección de errores; la segunda usa códigos de detección de errores.

Para entender la manera en que pueden manejarse los errores es necesario estudiar de cerca lo que es en realidad un error. Normalmente, un marco consiste en mbits de datos (es decir, n = m + r). A una unidad de n bits que contiene datos y bits de comprobación se le conoce como palabra código de n bits.

Dadas dos palabras código cualesquiera, digamos 10001001 y 10110001, es posible determinar cuántos bits correspondiente difieren. En este caso, difieren tres bits. Para determinar la cantidad de bits diferentes basta aplicar una operación OR EXCLUSIVO a las dos palabras código y contar la cantidad de bits 1 en el resultado. La cantidad de posiciones de bit en la que difieren dos palabras de código se llama distancia de HAMMING (Hamming 1950). Su significado es que, si dos palabras código están separadas una distancia de Hamming d, se requerirán d errores de un bit para convertir una en la otra.

En la mayoría de las aplicaciones de transmisión de datos, todos los 2 EXP m mensajes de datos posibles son legales, pero debido a la manera en que se calculan los bits de comprobación no se usan todas las 2 EXP n palabras código posibles. Dado el algoritmo de cálculo de los bits de comprobación, es posible construir una lista completa de palabras código legales y, en esta lista, encontrar las dos palabras código cuya distancia de Hamming es mínima. Esta distancia es la distancia de Hamming de todo el código.

Las propiedades de detección y corrección de errores de un código dependen de su distancia de Hamming. Para detectar d errores se necesita un código con distancia d + 1, pues con tal código no hay manera de que d errores de un bit puedan cambiar una palabra código válida a otra. Cuando el receptor ve una palabra código no válida, sabe que ha ocurrido un error de transmisión. De manera parecida, para corregir d errores se necesita un código de distancia 2d + 1, pues así las palabras código legales están tan separadas que, aun con d cambios, la palabra código original sigue estando más cercana que cualquier otra palabra código, por lo que puede determinarse única.

Como ejemplo sencillo de códigos de detección de errores, considere un código en el que se agrega un solo bit de paridad a los datos. El bit de paridad a los datos. El bit se escoge de manera que la cantidad de bits 1 en la palabra código sea par (o impar). Por ejemplo, cuando se envía 10110101 con paridad par añadiendo un bit al final, se vuelve 101101011, pero 10110001 se vuelve 101100010 con paridad par. Un código con un solo bit de paridad tiene una distancia de 2, pues cualquier error de un bit produce una palabra código con la paridad equivocada. Este sistema puede usarse para detectar errores individuales.

Como ejemplo sencillo de código de corrección de errores, considere un código con sólo cuatro palabras código válidas:

0000000000, 0000011111, 1111100000 y 1111111111.

Este código tiene una distancia de 5, lo que significa que puede corregir errores dobles. Si llega la palabra código 0000000111, el receptor sabe que el original debió ser 0000011111. Sin embargo, si un triple error cambia 0000000000 a 0000000111, el error no se corregirá adecuadamente.

Imagine que queremos diseñar un código con m bits de mensaje y r bits de comprobación que permitirá la corrección de todos los errores individuales. Cada uno de los 2 EXP m mensajes legales requiere n + 1 patrones de bits dedicados a él. Dado que la cantidad de patrones de bits es de 2 EXP n debemos tener (n+1)2 EXP m <= 2 EXP n. Usando n = m + r, este requisito se vuelve (m + r + 1) <= 2 EXP r . Dado m, esto impone un límite inferior a la cantidad de bits de comprobación necesarios para corregir errores individuales.

De hecho, este límite inferior teórico puede lograrse un método debido a Hamming (1950). Los bits de la palabra código se numeran consecutivamente, comenzando por el bit 1 a la izquierda. Los bits que son potencias de 2(1,2,4,8,16, etc.) son bits de comprobación. El resto (3,5,6,7,9,etc.) se rellenan con los bits de datos. Cada bit de comprobación obliga a que la paridad de un grupo de bits, incluyendo a él mismo, sea par (o impar). Un bit puede estar incluido en varios cálculos de paridad. Para ver a que bits de comprobación contribuye el bit de datos en la posición k, rescriba k como una suma de potencias de 2. Por ejemplo, 11 = 1 +2 +8 y 29 = 1 + 4 + 8 + 16. Se recomienda un bit solamente por los bits de comprobación que ocurren en su expansión (por ejemplo, el bit 11 es comprobado por los bits 1, 2, y 8).

Al llegar una palabra código, el receptor inicializará a cero un contador y luego examina cada bit de comprobación, k (k= 1,2,4,8,...) para ver si tiene la paridad correcta. Si no, suma k al contador. Si el contador es igual a cero tras haber examinado todos los bits de comprobación (es decir, si todos fueron correctos), la palabra código se acepta como válida. Si el contador es diferente de cero, contiene el número del bit incorrecto. Por ejemplo, si los bits de comprobación 1,2 y 8 tienen errores, el bit invertido es el 11, pues es el único comprobado por los bits 1,2 y 8. En la figura se muestra algunos caracteres ASCII de 7 bits codificados como palabras código de 11 bits usando el código de Hamming. Recuerde que los datos se encuentren en las posiciones de bit 3,5,6,7,9,10 y 11.

Carácter	ASCII	Bits de comprobación
H	1001000	00110010000
a	1100001	10111001001
m	1101101	11101010101
m	1101101	11101010101
i	1101001	01101011001
n	1101110	01101010110
g	1100111	11111001111
	0100000	10011000000
c	1100011	11111000011
o	1101111	00101011111
d	1100100	11111001100
e	1100101	00111000101
	Orden de Transmisión de bits.

Los códigos de Hamming sólo pueden corregir errores individuales. Sin embargo, hay un truco que puede servir para que los códigos de Hamming corrijan errores en ráfaga. Se dispone como matriz una secuencia de k palabras código consecutivas, con una palabra código por fila. Normalmente se transmitiría una palabra código a la vez, de izquierda a derecha . Para corregir los errores en ráfaga, los datos deben transmitirse una columna a la vez, comenzando por la columna de la extrema izquierda. Cuando todos los bits k han sido enviados, se envían la segunda columna, y así sucesivamente. Cuando el marco llega al receptor, la matriz se reconstruye, una columna a la vez. Si ocurre un error de longitud k, cuando mucho se habrá afectado 1 bit de cada una de las k palabras código; sin embargo, el código de Hamming puede corregir un error por palabra código; sin embargo, el código de Hamming puede corregir un error por palabra código, así que puede restaurarse la totalidad del bloque. Este método usa kr bits de comprobación para inmunizar bloques de km bits de datos contra una sola ráfaga de errores de longitud k o menos.

Código de detección de errores.

Los códigos de corrección de errores a veces se utilizan para la transmisión de datos; por ejemplo, cuando el canal es simplex, por lo que no pueden solicitarse retransmisiones. Sin embrago, con mayor frecuencia se prefiere la detección de errores seguida de la retransmisión porque es más eficiente. Como ejemplo simple, considere un canal en el que los errores son aislados y la tasa de errores es de 10 EXP –6 por bit. Sea el tamaño de bloque 1000 bits. Para proporcionar corrección de errores en bloques de 1000 bits se requieren 10 bits de comprobación; un megabit de datos requerirá 10,000 bits de comprobación. Para detectar un solo bloque con 1 bit de error, basta con un bit de paridad por bloque. Por cada 1000 bloques se tendrá que retransmitir un bloque extra (1001 bits). El gasto extra del método de detección de errores + retransmisión es de solo 2001 bits por megabit de datos, contra 10,000 bits con un código de Hamming.

Si se agrega un solo bit de paridad a un bloque y el bloque viene muy alterado por una ráfaga de errores prolongada, la probabilidad de que se detecte el error es de 0.5 , lo que difícilmente es aceptable. Puede mejorarse mucho la probabilidad considerando a cada bloque por enviar como una matriz rectangular de n bits de ancho y k bits de alto. Se calcula por separado un bit de paridad para cada columna y se agrega a la matriz como última fila. La matriz se transmite entonces fila por fila. Al llegar el bloque, el receptor comprueba todos los bits de paridad. Si cualquiera de ellos está mal, solicita la retransmisión del bloque.

Este método puede detectar una sola ráfaga de duración n, pues sólo se cambiará un bit por columna. Sin embargo, una ráfaga de duración n+1 pasará sin ser detectada si se invierte el primer bit, el último bit y todos los demás bits están mal; sólo implica que cuando menos el primero y el último están mal.) Si el bloque está muy alterado por una ráfaga continua o por accidente, la paridad correcta es de 0.5, por lo que la probabilidad de aceptar un bloque alterado cuando no se debe es de 2 EXP –n.

Aunque el esquema anterior puede ser adecuado en algunos casos, en la práctica se usa otro método muy difundido: el código polinómico se basa (también conocido como código de redundancia cíclica o código CRC) Los códigos polinómicos se basan en el tratamiento de cadenas de bits como representaciones de polinomios con coeficientes de un polinomio con k que van de x EXP k-1 a x EXP 0. Se dice que tal polinomio es de grado k-1 . El bit mayor (más izquierdo) es el coeficiente de x EXP (k-1) , el siguiente bit es el coeficiente de x EXP (k-2) y así sucesivamente. Por ejemplo, 110001 tiene 6 bits y por tanto representa un polinomio de seis términos con coeficientes 1,1,0,0,0 y 1 : x EXP 5 + x EXP 4 + x EXP 0.

La aritmética polinómica se hace módulo 2, de acuerdo con las reglas de la teoría de campos algebraicos. No hay acarreos para la suma, ni préstamos para la resta. Tanto la suma como la resta son idénticas a un OR EXCLUSIVO. Por ejemplo:

10011011	00110011	11110000	01010101
+11001010	+11001101	-10100110	-10101111
-----------------	------------------	-----------------	-----------------
01010001	11111110	01010110	11111010

La división se lleva a cabo de la misma manera que en binario, excepto que la resta se hace módulo 2, igual que antes. Se dice que un divisor “cabe” en un dividendo si el dividendo tiene tantos bits como el divisor.

Control de errores

Un circuito de comunicación de datos puede ser tan corto, de unos cuantos pies o, tan largo, de varios miles de millas; el medio de transmisión puede ser tan sencillo, como pedazo de cable o, tan complejo, como un sistema de microondas, satélite o fibra óptica. Por lo tanto, debido a las características, no ideales que están asociadas con cualquier sistema de comunicación, es inevitable que ocurran errores y es necesario desarrollar e implantar procedimientos para el control de errores. El control de errores puede dividirse en dos categorías generales: Detección de errores y Corrección de errores.

Detección de errores

La detección de errores es simplemente el proceso de monitorear la información recibida y determinar cuando un error de transmisión ha ocurrido. Las técnicas de detección de errores no identifican cual bit (o bits) es erróneo, solamente indica que ha ocurrido un error. El propósito de la detección de errores no es impedir que ocurran errores, pero previene que los errores no detectados ocurran. Como reacciona un sistema a los errores de transmisión, depende del sistema y varía considerablemente. Las técnicas de detección de errores más comunes usados para los circuitos de comunicación de datos son: Redundancia, Codificación de cuenta exacta, Paridad, Chequeo de redundancia vertical y Longitudinal, y Chequeo de redundancia cíclica.

Redundancia.- La Redundancia involucra transmitir cada carácter dos veces. Si el mismo carácter no se recibe dos veces sucesivamente, ha ocurrido un error de transmisión. El mismo concepto puede usarse para los mensajes. Si la misma secuencia de caracteres no se recibe dos veces sucesivamente, en exactamente el mismo orden, ha ocurrido un error de transmisión.

Codificación de cuenta exacta.- Con la codificación de cuenta exacta, el número de unos, en cada carácter, es el mismo. Cada carácter tiene tres unos en el y, por lo tanto, una cuenta sencilla de la cantidad de unos recibidos, en cada carácter, determina si ha ocurrido un error de transmisión.

Paridad.- La paridad es probablemente el esquema de detección de error, mas sencillo, usado para los sistemas de comunicación de datos y se usa con cheque de redundancia vertical y horizontal. Con la paridad, un solo bit (llamado bit de paridad) se agrega a cada carácter para forzar el total de números unos en el carácter, incluyendo el bit de paridad, para que sea un numero impar (paridad impar) o un numero par (paridad par). Por ejemplo, el código ASCII para la letra “C” es 43 hex o P1000011 binario, con el bit P representando el bit de paridad. Hay tres unos en el código, no contando el bit de paridad. Si se usa la paridad impar, el bit P se hace un 0, manteniendo el número total de unos en tres, un número impar. Si se usa la paridad par, el bit P se convierte en 1 y el número total de unos es cuatro, un número par.

Observando más de cerca la paridad, puede verse que el bit de paridad es independiente del número de ceros en el código y no es afectado por pares de unos. Para la letra “C”, si todos los bits 0 se descartan, el código de P1_____11. Para la paridad impar, el bit P, aun es un 0 y para la paridad par, el bit P aun es un 1. Si los pares de unos, también se excluyen, el código es o P1_______, P______1, o P_____1_. Nuevamente, para la paridad impar, el bit P es un 0, y para la paridad par, el bit P es un 1.

La definición de paridad es equivalencia o igualdad. Una compuerta lógica que determina cuando todas sus entradas son iguales, es la compuerta XOR. Con una compuerta XOR, si todas las entradas son iguales (ya sea todos ceros o todos unos) la salida es un 0. Si todas las entradas son iguales no son iguales, la salida es un 1. Esencialmente, ambos circuitos pasan por un proceso de comparación eliminando los ceros y pares de unos. El circuito utiliza una comparación secuencial (serial), mientras que el circuito utiliza una comparación combinada (paralela). Con el generador de paridad b0 usa XOR con b₁, la salida usa XOR con b₂, etc. La salida de la última operación XOR se compara con un bit polarizado. Si se desea la paridad par, el bit polarizado se convierte en 0 lógico. Si se desea la paridad impar, el bit polarizado se hace 1 lógico La salida del circuito es el de paridad, el cual se agrega al código de caracteres. Con el generador de paridad paralelo, las comparaciones se hacen en capas o niveles. Los pares de bits (b₀ y b₁, b₂ y b₃, etc.) usan XOR. Los resultados de las salidas XOR de primer nivel se utilizan entonces juntos. El proceso continua, hasta que solo un bit permanece, el cual usa XOR con el bit polarizado. Nuevamente, si se desea la paridad par, el bit polarizado se hace 0 lógico y si se desea la paridad impar, el bit polarizado se hace 1 lógico.

Un chocador de paridad usa el mismo procedimiento que un generador de paridad, excepto que la condición de lógica de la ultima comparación se usa para determinar si una violación de paridad ha ocurrido (para la paridad impar un 1 indica un error y un 0 indica que no hay error; para la paridad par, un 1 indica un error y un 0 indica que no hay error).

La ventaja principal de la paridad es la simplicidad. La desventaja es que cuando un numero par de bits se recibe erróneamente, el checador de paridad no lo detendrá (o sea, si las condiciones de lógica de 2 bits se cambian, la paridad permanece igual). Consecuentemente, la paridad en un periodo largo de tiempo, detectara solos el 50% de los errores de transmisión (esto asume una probabilidad igual, que un numero de bits, par o impar, podría estar en error).

Comprobación de paridad.- El esquema mas sencillo para detectar errores consiste en añadir un BIT de paridad al final del bloque de datos. (Por ejemplo si hay un número par de BITS 1, se le añade un BIT 0 de paridad y si son impares, se le añade un BIT 1 de paridad). Un ejemplo típico es la transmisión de caracteres, en la que se añade un BIT de paridad por cada carácter IRA de 7 BITS. El valor de este BIT se determina de tal forma que el carácter resultante tenga un numero impar de unos (paridad impar) o un numero par (paridad par). Así por ejemplo si el transmisor esta transmitiendo una G en IRA (1110001) y se utiliza paridad impar, se añadirá un 1 y se transmitirá 11100011. el receptor examina el carácter recibido y , si el numero total de unos es impar supondrá que no ha habido errores. Si un BIT o cualquier numero impar de BITS se invierte erróneamente durante la transmisión entonces el receptor detectara un error. Nótese que si dos o cualquier numero par de BITS se invierten debido a un error, aparecerá un error no detectado. Generalmente, se utiliza paridad par para la transmisión síncrona y paridad impar para la asíncrona. La utilización de BITS de paridad no es infalible, ya que los impulsos de ruido son a veces lo suficientemente largos como para destruir mas de un BIT, especialmente a velocidades de transmisión altas. Pero puede ocurrir que el propio BIT de paridad sea cambiado por el ruido o incluso que más de un BIT de datos sea cambiado , con lo que el sistema de detección fallará .

Chequeo de redundancia vertical y horizontal.- El Chequeo de redundancia vertical (VRC), es un esquema de detección de errores que usa la paridad para determinar si un error de transmisión ha ocurrido dentro de un carácter. Por lo tanto, el VRC a veces se llama paridad de carácter. Con el VRC, cada carácter tiene un bit de paridad agregado a el, antes de la transmisión. Puede usar paridad par o impar. El ejemplo mostrado bajo el tema “paridad” involucrando el carácter de ASCII “C”, es un ejemplo de cómo se usa el VRC.

El chequeo de redundancia horizontal y longitudinal (HRC o LRC), es un esquema de detección de errores que utiliza la paridad para determinar si un error de transmisión ha ocurrido en un mensaje y, por lo tanto, a veces es llamado paridad de mensaje. Con el LRC cada posición de bit tiene un bit de paridad. En otras palabras, b₀ de cada carácter en el mensaje usa XOR con b0 de todos los demás caracteres en el mensaje. De manera semejante, b₁, b₂, y así sucesivamente, utilizan XOR con sus bits respectivos de todos los demás caracteres en el mensaje. Esencialmente, el LRC es el resultado de usar XOR con los caracteres que componen un mensaje, mientras que el VRC es el uso de XOR en los bits con un solo carácter. Con el LRC, solo la paridad par será usada.

La secuencia del bit en el LRC se calcula en el transmisor, antes de enviar la información, después se transmite como si fuera el último carácter del mensaje. En el receptor, LRC se recalcula en los datos y el LRC recalculado se compara con el LRC transmitido con el mensaje. Si son iguales, se asume que ningún error de transmisión ha ocurrido. Si son diferentes, un error de transmisión debe haber ocurrido. El ejemplo siguiente muestra como el VRC y el LRC son determinados.

EJEMPLO:

Determine el VRC y el LRC para el siguiente mensaje codificado ASCII: THE CAT (el gato). Utilice la paridad impar para el VRC y paridad par para el LRC.

SOLUCION

Carácter		T	H	E	Sp	C	A	T	LRC
Hex		54	48	45	20	43	41	54	2F
LSB	b0	0	0	1	0	1	1	0	1
	b1	0	0	0	0	1	0	0	1
Código	b2	1	0	1	0	0	0	1	1
ASCII	b3	0	1	0	0	0	0	0	1
	b4	1	0	0	0	0	0	1	0
	b5	0	0	0	1	0	0	0	1
MSB	b6	1	1	1	0	1	1	1	0
VRC	b7	0	1	0	0	0	1	0	0

El LRC es 2FH o 00101111 binario. En ACII, este es el carácter /.

El bit VRC para cada carácter se calcula en dirección vertical y los bits del LRC se calculan en dirección horizontal. Este es el mismo esquema que fue usado con las primeras cintas de papel para teletipo y tarjetas de perforación y subsecuentemente en las aplicaciones de comunicación de datos actuales.

El grupo de caracteres que componen el mensaje (es decir, el gato) a menudo se llama bloque de información. Por lo tanto, la secuencia del bit para el LRC frecuentemente se llama carácter de chequeo de bloque (SCC) o una secuencia de chequeo de bloque (BCS). El BCS es mas apropiado, porque el LRC no tiene función como un carácter (o sea, no es un carácter alfa/numérico, grafico o enlazado con datos); el LRC es simplemente una secuencia de bits usada para la detección de errores.

Históricamente, LRC detecta entre 75% y 98% de todas las transmisiones de errores. El LRC no detectara errores de transmisión cuando un número par de caracteres tienen un error en la misma posición del bit. Por ejemplo, si b₄ en dos diferentes caracteres esta en error, el LRC aun es valido, aunque hayan ocurrido múltiples errores de transmisión.

Si los VRC y LRC se usan simultáneamente, la única vez que un error no se detecta es cuando un numero par de bits, en un numero par de caracteres, estuviera en un error y las mismas posiciones del bit, en cada carácter, están en error, lo cual no es muy probable que suceda. El VRC no identifica cual bit esta en error en un carácter, y el LRC no identifica cual carácter tiene un error en el. Sin embargo, para los errores de bit sencillo, el VRC usado junto con el LRC, identifica cual bit esta en un error. De otra manera, los VRC y LRC solo identifican que un error ha ocurrido.

Revisión de redundancia cíclica.- Probablemente, el esquema más confiable para la detección de errores es el chequeo de redundancia cíclica (CRC). Con CRC, aproximadamente el 99.95% de todos los errores de transmisión se detectan. El CRC se usa generalmente con códigos de 8 bits, tales como EBCDIC o códigos de 7 bits, cuando no se usa paridad. Dado un bloque o mensaje de k-BITS, el transmisor genera una secuencia de n-BITS denominada secuencia de comprobación de la trama FCS (Frame Check Secuence), de tal manera que la trama resultante con n+ k BITS sea divisible por algún numero predeterminado. El receptor entonces dividirá la trama recibida por ese numero y si no hay residuo en la división se supone que no ha habido errores. Este proceso puede hacerse bien por software o bien por un circuito hardware (mas rápido).

En E.U., el código Cremas común es el CRC-16, el cual es idéntico al estándar internacional, CCITT V.41. Con el CRC-16, se utilizan 16 bits para el BCS. Esencialmente, el carácter CRC es el sobrante de un proceso de división. Un mensaje de datos polinomico G(x) se divide por una función de polinomico del generador P(x), el cociente se descarta, y el residuo se trunca en 16 bits y se agrega al mensaje como el BCS. Con la generación de CRC, la división no se logra con un proceso de división aritmética estándar. En vez de usar una resta común, el residuo se deriva de una operación de XOR. En el receptor, el flujo de datos y el BCS se dividen por la misma función de generación P(x). Si ningún error de transmisión ha ocurrido, el residuo será cero. El polinomio generado para CRC-16 es

P(x) = x¹⁶ + x¹² + x⁵ + x⁰

En donde x⁰ = 1

El número de bits en el código CRC es igual al exponente más alto del polinomio generado. Los exponentes identifican las posiciones del bit que contiene un 1. Por lo tanto, b₁₆, b₁₂, y b₀ son todos unos y todas las demás posiciones de bits son ceros.

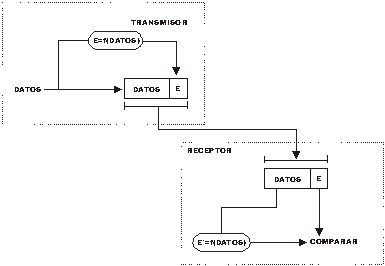
La Fig. muestra el diagrama a bloques para un circuito que genera un CRC-16 BCS, para el estándar CCITT V.41. Observe que para cada posición de bit del polinomio generado es donde hay un 1 se coloca una compuerta excepto por x⁰.

Ejemplo 13-2

Determine el BCS para los siguientes polinomios generadores de datos y CRC.

Datos G(x) = x⁷ + x⁵ + x⁴ + x² + x¹ + x⁰ o 10110111

CRC P(x) = x⁵ + x⁴ + x¹ + x⁰ o 110011

Solución: Primero G(x) es multiplicado por el número de bits en el código CRC, 5.

x⁵ (x⁷ + x⁵ + x⁴ + x² + x¹ + x⁰) = x¹² + x¹⁰ + x⁹ + x⁷+ x⁶ + x⁵ = 1011011100000

Después divida el resultado por P(x)

11010111

110011| 1011011100000

110011

111101

110011

111010

110011

100100

110011

101110

110011

111010

110011

01001 = CRC

El CRC se agrega a los datos para dar el siguiente flujo de datos transmitido.

G(x) CRC

10110111 01001

En el receptor, los datos transmitidos son nuevamente divididos por P(x).

11010111

110011| 1011011100001

110011

111101

110011

111010

110011

100110

110011

101010

110011

110011

110011

000000 = residuo = 0

Ningún error ocurrido

Corrección de errores

Esencialmente, hay tres métodos de corrección de errores: Sustitución de símbolos, Retransmisión y Seguimiento de corrección de un error.

Sustitución de Símbolos.- La sustitución de símbolos se diseño para usarse en un ambiente humano: en donde hay un ser humano, en la terminal de recepción, para analizar los datos recibidos y tomar decisiones sobre su integridad. Con la sustitución de símbolos, si un carácter se recibe en error, en vez de revertirse a un nivel superior de corrección de errores o mostrar el carácter incorrecto, un carácter único que es indefinido por el código de caracteres, tal como un signo de interrogación invertido (؟), se sustituye por el carácter malo. Si el carácter erróneo no puede distinguirse por el operador, la retransmisión es para llamada (o sea, la sustitución de símbolos es una forma de retransmisión selectiva). Por ejemplo, si el mensaje “Nombre” tenia un error en el primer carácter, se mostraría como “؟ombre”. Un operador puede discernir el mensaje correcto por inspección, y la retransmisión no es necesaria. Sin embargo, si el mensaje “$؟,000.00” se recibiera, un operador no podría determinar el carácter correcto y la retransmisión seria requerida.

Retransmisión.- Es volver a enviar un mensaje, cuando es recibido en error, y la terminal de recepción automáticamente pide la retransmisión de todo el mensaje. La retransmisión frecuentemente se llama ARQ, el cual es un término antiguo de la comunicación de radio, que significa petición automática para retransmisión. ARQ es probablemente el método más confiable de corrección de errores, aunque no siempre es el más eficiente. Las dificultades en el medio de transmisión ocurren en ráfagas. Si se usan mensajes cortos requieren de más reconocimientos y regresos de línea que los mensajes largos. Los reconocimientos y regresos de línea para el control de errores so formas de encabezamientos (caracteres diferentes a los datos que se deben transmitir). Con los mensajes largos, menos tiempo de regreso es necesario, aunque la probabilidad de que un error de transmisión ocurra es mayor que para los mensajes cortos. Se puede mostrar, de manera estadística, que los bloques de mensajes entre 256 y 512 caracteres son de tamaño óptimo, cuando se utiliza ARQ para corrección de errores.

Seguimiento de corrección de error.- El Seguimiento de corrección de error (FEC), es el único esquema de corrección de error que detecta y corrige los errores de transmisión, del lado receptor, sin pedir retransmisión.

Con FEC, se agregan bits al mensaje, antes de la transmisión. Un código de corrección de errores popular, es el código de Hamming, desarrollado por R.W. Hamming, en los laboratorios Bell. El número de bits en el código de Hamming depende del número de bits en el carácter de datos. El número de bits de Hamming que debe agregarse a un carácter se determina de la siguiente expresión:

2ⁿ ≥ m + n + 1

En donde: n = numero de bits de Hamming m = numero de bits en el carácter de datos

Ejemplo 13-3

Para una cadena de datos de 12-bits de 101100010010, determine el número de bits de Hamming requerido, coloque arbitrariamente los Bits de Hamming en la cadena de datos, determine la condición de cada bit de Hamming, asuma un error de transmisión de bit sencillo arbitrario y compruebe que el código de Hamming detectara el error.

Solución: Sustituyendo en la ecuación, el numero de bits de Hamming es

2ⁿ ≥ m + n + 1

para n = 4:

2⁴ = 16 ≥ m + n + 1 = 12 + 4 + 1 = 17

16 < 17; por lo tanto, 4 bits de hamming son insuficientes.

Para n = 5:

2⁵ = 32 ≥ m + n + 1 = 12 + 5 + 1 = 18

32 > 18; por lo tanto, 5 bits de Hamming son insuficientes para llenar el criterio de la ecuación. Por lo tanto, un total de 12 + 5 = 17 bits componen el flujo de datos.

Coloque arbitrariamente 5 bits de Hamming en el flujo de datos:

17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1

H 1 0 1 H 1 0 0 H H 0 1 0 H 0 1 0

Para determinar la condición lógica de los bits de Hamming, exprese todas las posiciones de bit que contienen un 1, como un numero binario de 5 bits y usando XOR juntos.

Posición de bit	Numero binario
2	00010
6	00110
XOR	00100
12	01100
XOR	01000
14	01110
XOR	00110
16	10000
XOR	10110	= Código de Hamming

El flujo de datos codificados de 17 bits se convierte en

H				H				H	H				H
1	1	0	0	0	1	0	0	1	1	0	1	0	0	0	1	0

Asuma que durante la transmisión, un error ocurre en la posición de bit 14. El flujo de datos recibido es

1 1 0 0 0 1 0 0 1 1 0 1 0 0 0 1 0

En el receptor, para detreminar el bit en error, extraiga los bits de Hamming y usando XOR con el código binario para cada posición de bit de datos que contiene un 1.

Posición de bit	Numero binario
Código de Hamming	00010
2	00110
XOR	10100
6	00110
XOR	10010
12	01100
XOR	11110
16	10000
XOR	01110	= binario 14

La posición de bit 14 fue recibida en error. Para arreglar el error, simplemente complemente el bit 14.

El código de Hamming descrito aquí, detectara solo errores de un solo bit. No se puede usar para identificar errores de bits múltiples o errores en los bits de Hamming. El código de Hamming, como todos los códigos FEC, requiere de la adición de los bits a los datos, alargando consecuentemente el mensaje transmitido. El propósito de los códigos FEC es reducir o eliminar el tiempo gastado de retransmisiones. Obviamente, se negocia entre ARQ y FEC, y los requerimientos del sistema determinan que método es mejor para un sistema en particular. El FEC frecuentemente se usa para transmisiones sencillas a muchos receptores, cuando los reconocimientos no son prácticos.

Deteccion y correccion de errores

Una de las metas mas importantes en el diseño de transmisión de datos es reducir al mínimo el error; la tasa de error se define como la relación entre la cantidad de bits que se reciben incorrectamente contra el total de bits que se transmite. En muchos circuitos de datos el objetivo de diseño es lograr que la tasa de error sea menor a un error 1x10⁵ (se expresa frecuentemente como 1x10^-5 ) y para los circuitos telegráficos, un error en 1x10⁴.

El método para reducir al mínimo la tasa de error es tener un canal de transmisión “perfecto”, que no introduzca errores en la información que se transmite hasta la salida del receptor. Sin embargo, no se puede lograr este canal perfecto. Además de la mejora en los parámetros mismos del canal de transmisión, la tasa de error se puede reducir mediante ciertas formas de redundancia sistemática. En el antiguo código Morse se enviaban dos veces las palabras sobre un circuito defectuoso, lo cual es redundancia en su forma más simple. Naturalmente, se tomaba el doble de tiempo para enviar el mensaje, además de que no es rentable si se compara la cantidad de palabras útiles que se reciben por minuto contra la ocupación del canal.

Lo siguiente ilustra el compromiso entre la redundancia y la eficiencia del canal: La redundancia se puede incrementar a un grado tal que la tasa de error se acerque a cero, pero la transferencia de información o eficiencia sobre el canal también se aproximara a cero. En consecuencia, la redundancia que no sea sistemática es un desperdicio y reduce únicamente la tasa de comunicación útil. Por otro lado, se puede obtener la máxima eficiencia en el sistema de transmisión digital si de la corriente de bits se transmite se elimina la redundancia y otros elementos de código como son los de “arranque” y “fin”, los bits de paridad y otros bits de “encabezado”. Obviamente hay un compromiso entre costo y beneficio en algún punto entre la máxima eficiencia sobre un circuito de datos y la redundancia que se añade sistemáticamente.

Eficiencia.- La Eficiencia en un canal de datos expresa la cantidad de datos que pasan a través de el. El término es la medida de los datos útiles que pasan a través del enlace de comunicación, estos datos se pueden usar directamente en una computadora o ETD (equipo terminal de datos).

De lo anterior se concluye que la eficiencia en un circuito especifico varia con la tasa base de datos, se e relaciona con la tasa de error y el tipo de error que se encuentra (ya sea en ráfaga o aleatorio) y varia de acuerdo con el tipo de sistema de detección y corrección de errores que se usa, el tiempo para manejar el mensaje y la longitud del bloque a partir del cual se toman los bits de encabezados como son los de paridad, banderas, verificaciones de redundancia cíclicas, etc.

Naturaleza de los Errores.- En la transmisión de datos, un error es un bit que no se recibe correctamente. Por ejemplo, se transmite “1” en un cierto espacio de tiempo, pero el elemento que se recibe en tal espacio de tiempo se interpreta como “0”. Los errores en los bits se presentan tanto en la forma de errores aleatorios únicos o como en ráfaga de errores. Por ejemplo, las descargas eléctricas u otra forma de ruido de pulsos ocasionan frecuentemente ráfagas de errores en las que muchos de los bits contiguos presentan gran cantidad de bits erróneos. El IEEE define la ráfaga de errores como “un grupo de bits en el que dos bits sucesivos con error están separados por una cantidad de bits correctos que es inferior a una cantidad establecida”.

Definición de detección y corrección de errores.- La detección de errores indica que símbolo se recibe con error. La paridad se usa principalmente para la detección de errores; sin embargo, los bits de paridad añaden redundancia y, en consecuencia, se reduce la eficiencia del canal.

La corrección de errores repara el error que se detecta. Básicamente existen dos tipos de técnicas para la corrección de errores: la que actúa hacia adelante (CEA) y la bidireccional [solicitud automática de repetición (SAR)]; en este último sistema se usa un canal de retorno (canal hacia atrás). Cuando se detecta un error, el receptor lo indica al transmisor sobre el canal hacia atrás y se transmite de nuevo el bloque* de información que contiene el error. En la corrección de errores con acción hacia adelante (CEA) se utiliza un tipo de codificación que solo permite una cantidad limitada de errores para su corrección en el extremo receptor mediante logística (software) o circuiteria (hardware) que se implanta en ambos extremos.

Existen varios arreglos o técnicas disponibles para la detección de errores. Todos los métodos para la detección de errores implican alguna forma de redundancia como, por ejemplo, los bits o secuencias adicionales para informar al sistema la presencia de algún o algunos errores. La paridad de carácter tiene como inconveniente su debilidad. Generalmente los ingenieros de sistemas de datos se refieren a tal paridad como verificación de redundancia vertical (VRV).

En otra forma detección de errores se utiliza la verificación de redundancia longitudinal (VRL), la cual se usa en la transmisión por bloques, en la que un mensaje consta de uno o más bloques. Recuerdese que un bloque es un grupo especifico de dígitos o caracteres de datos que se envían como “paquete”. El carácter VRL, que se conoce también como CVB o carácter de verificación de bloque, se añade al final de cada bloque. El CVB verifica la cantidad total de “1” y “0” en las columnas de bloque (verticalmente). En el extremo receptor se suman los “1” (o los “0”) del bloque según la convención de paridad en el sistema; si la suma no coincide con el CVB existe un error (o errores) en el bloque, *El “bloque” es el grupo de dígitos (caracteres de datos) que se transmiten como una sola unidad sobre la cual se aplica generalmente un procedimiento de codificación con fines de sincronía y control de error.

Con la VLR se mejora mucho el problema de los errores que no se detectan y que pueden escapar a la VRV si se usa sola; sin embargo, el método VRL no es a prueba de errores, ya que usa el mismo razonamiento que el VRV. Supóngase que ocurre un error de manera que se sustituyen dos “1” por dos “0” en las posiciones del segundo y tercer bits de los caracteres “1” y “3” de un cierto bloque. En este caso, el CVB se lee correctamente en el extremo receptor y el error escapa también a la VRV. Obviamente, en un sistema en el que se usa la VRL y la VRV es mas difícil que pasen los errores sin detectar que en uno en que solo se use una verificación. Un método mas efectivo para la detección de errores es la VRC, la cual se basa en un código cíclico y se usa en la transmisión por bloques con un CVB. En este caso, el CVB que se transmite representa el residuo de la división del bloque de mensaje entre un “polinomio generador”. Matemáticamente, el bloque de mensaje se puede tratar como una función, por ejemplo:

a_nXⁿ + a_n-1X^n-1 + a_n-2X^n-2 + …..+ a₁X + a₀

donde los coeficientes se ajustan para que representen un número binario. Considérese el número binario 11011, el cual se representa de manera polinómica:

1	1	0	1	1
a4	a3	a2	a1	a0

y se convierte en:

X⁴ + X³ + X + 1

o considérese este otro ejemplo:

0	1	1	0	1
a4	a3	a2	a1	a0

que se convierte en:

X³ + X + 1

El carácter VRC se usa como el CVB y es el residuo del polinomio de datos cuando se divide entre el polinomio generador. Entonces, si el polinomio de datos D(X) se divide entre el polinomio generador G(X), resulta un cociente Q(X) y un residuo R(X) polinomicos, o:

D(X) = Q(X) + R(X)

G(X) G(X)

En la mayoría de las aplicaciones, la longitud del carácter VRC es de 16 bits o dos bytes de 8 bits. En la actualidad se usan generalmente tres polinomios generadores estándar:

1. VRC-16 (ANSI): X¹⁶ + X¹⁵ + X⁵ + 1

2. VRC (CCITT) : X¹⁶ + X⁵ + 1

3. VRC-12: X¹² + X¹¹ + X³ + 1

Naturalmente, si al comparar la cantidad del CVB en el extremo receptor es diferente a la del CVB del extremo transmisor existe un error (o errores) en el bloque que se recibe.

En la referencia 34 se establece que la VCR-12 proporciona detección de errores de ráfagas de hasta 12 bits de longitud y, adicionalmente, de pueden detectar hasta el 99.955% de ráfagas de error con longitud hasta de 16 bits. La VCR-16 proporciona detección de ráfagas de hasta 16 bits de longitud y una detección adicional del 99.955% de ráfagas de error con longitud mayor a los 16 bits. En todo sistema de transmisión habrá ruido, independientemente de cómo haya sido diseñado. El ruido dará lugar a errores que modificaran uno o varios bits de la trama.

Cuanto mayor es la trama que se transmite, mayor es la probabilidad de que contenga algún error. Para detectar errores, se añade un código en función de los bits de la trama de forma que este código señale si se ha cambiado algún BIT en el camino Este código debe de ser conocido e interpretado tanto por el emisor como por el receptor.

Los errores en las troncales digitales son raros pero son comunes en la transmisión inalámbrica. Las probabilidades en términos de los errores en las tramas transmitidas se definen como sigue:

P_b: probabilidad de un BIT erróneo, también denominada tasa de error por BIT VER (BIT Error Rate).

P₁: probabilidad de que una trama llegue sin errores.

P₂: probabilidad de que una trama llegue con uno o mas errores no detectables.

P₃: probabilidad de que una trama llegue con uno o mas errores detectables pero sin errores indetectables.

Primero se toma el caso en el que no se toman medidas para detectar errores. En ese caso, la probabilidad de errores detectables P₃ es cero. Para calcular las otra probabilidades se supondrá que todos los BITS tienen una probabilidad de error P_b constante, independientemente de donde estén situados en la trama.

Entonces se tiene que:

P₁ = (1-P_b)^F F: numero de BITS por trama

P₂ = 1-P₁

En otras palabras, la probabilidad de que una trama llegue sin ningún BIT erróneo disminuye al aumentar la probabilidad de que un BIT sea erróneo; además, la probabilidad de que una trama llegue sin errores disminuye al aumentar la longitud de la misma; cuanto mayor es la trama, mayor numero de BITS tendrá, y mayor será la probabilidad de que alguno de los BITS sea erróneo.

Dada una trama de BITS se añaden BITS adicionales por parte del transmisor para formar un código con capacidad de detectar errores. Este código se calculara en función de los otros BITS que se vayan a transmitir. El receptor realizara el mismo calculo y comparara los dos resultados. Se detectara un error si y solamente si los dos resultados mencionados no coinciden. Por tanto, P₃ es la probabilidad de que la trama que contenga errores y el sistema los detecte. P₂ se denomina tasa de error residual, y es la probabilidad de que no se detecte un error aunque se este usando un esquema de detección de errores.

En algunos medios (por ejemplo, el radio) los errores ocurren en grupos (en vez de individualmente). Un grupo inicia y termina con bits invertidos, con algún subconjunto (posiblemente nulo) de los bits intermedios también invertidos.

Un CODEWORD de n BITS consiste en un conjunto de m BITS de datos y r BITS de redundancia o chequeo.

Corrección de errores con acción hacia delante.- En la corrección de errores con acción adelante (CEA) se utilizan ciertos códigos binarios que se diseñan para corregir por si mismos los errores que introduce el medio de transmisión que se utiliza. Con esta forma de corrección de error en la estación receptora se pueden reconstruir los mensajes que contengan error.

Los que se usan en la CEA se dividen en dos amplias clases: Códigos de bloque y Códigos convulcionales. En los códigos de bloque se toman k bits de información cada vez y se añaden c bits de paridad, la verificación se hace sobre las combinaciones de los k bits de información; un bloque consta de n = k + c dígitos; el código consta de k palabras, cada una con n dígitos de extensión. Cuando se usan para transmisión de datos, los códigos de bloque pueden ser sistemáticos. Un código sistemático es aquel en que los bits de información ocupan las primeras k posiciones del bloque y los siguen (n-k) dígitos de verificación.

Otro código de bloque es el código de grupo en el que la suma en modulo 2 de dos palabras cualesquiera de n bits del código es otra palabra del mismo. La suma en modulo 2 se denota por el símbolo + y consiste en la suma binaria sin el “acarreo”, o sea que 1 + 1 = 0, sin llevar 1; cuando se suman 10011 y 11001 en modulo 2 el resultado es 01010.

La distancia mínima de sobre seguridad (Hamming) es la medida de la capacidad de un código para detectar y corregir errores. Esta “distancia” es la cantidad mínima de dígitos en la que difieren dos palabras codificadas. Por ejemplo, para detectar un error de E dígitos se necesita que el código tenga la distancia mínima de sobreseguridad de (E+1); para corregir un error de E dígitos la distancia mínima de sobreseguridad del código debe ser (2E+1). Un código cuya distancia de sobreseguridad es de 4 puede corregir un solo error y detectar dos dígitos con error.

El código de convulsión (convulcional) es otra forma de codificar que se usa para detección y corrección de errores. Como su nombre lo indica, es un código que se enrolla o se convulsiona sobre otro, es decir, es la convulción de una corriente de datos de entrada y la función de respuesta de un codificador. Generalmente, el codificador esta compuesto por registros de corrimiento y se usan sumadores en modulo 2 para verificar los dígitos, cada uno de los cuales es función binaria de un subconjunto particular de los dígitos de información del registro de corrimiento.

La función de error se puede mejorar mediante el uso de un microprocesador en el decodificador; la decisión entre marca o espacio no es tan estricta o irrevocable, más bien se le conoce como decisión “suave”. En este caso, se añade una etiqueta de 3 bits a cada digito que se recibe para indicar en el demodulador el nivel de confiabilidad de la decisión antes de procesar; después del procesamiento, cuando se indican los errores, se cambian los bits con el nivel mas bajo de confiabilidad de 0 a 1 o de 1 a 0, según sea el caso.

Los códigos que se estudiaron hasta este punto son efectivos para detectar y corregir errores aleatorios que se deben exclusivamente a las perturbaciones del ruido Gaussiano blanco aditivo y a la limitación en la potencia de la señal. En muchos circuitos de transmisión se encuentran ráfagas de ruido en las que los disparos de ruido exceden en duración a 1 o 2 bits. Naturalmente, una manera de combatir este ruido es prolongar la duración del bit. Sin embargo, tales ráfagas pueden tener una duración de 10 a 100 ms y los “disparos” se deben típicamente al ruido de impulsos.

El código Hagelberger es un código de corrección de errores con acción adelante para combatir con eficacia las ráfagas de error. Para usar este código se deben cumplir dos requisitos: La longitud de la ráfaga no debe ser de más de 8 bits y debe haber al menos 91 dígitos correctos entre ráfagas, pero se reduce la eficiencia al 75% o, dicho en otras palabras, se añade redundancia con lo que 1 de cada 4 es de verificación.

Corrección de errores con canal de retroalimentación.- La corrección de errores bidireccional o con retroalimentación se usa ampliamente en los circuitos actuales de datos y sobre algunos telegráficos; esta forma de corrección de errores se conoce como SAR. Las siglas se derivan de la antigua señal Morse y telegráfica “solicitud automática de repetición” (automatic repeat request). En la mayoría de los sistemas de datos modernos se usa la transmisión en bloque; este tiene la longitud conveniente de caracteres para su envío como entidad; la longitud “conveniente” es una importante consideración. La cantidad “conveniente” se relaciona con la tarjeta “IBM” estándar de 80 columnas; con 8 bits por columna es conveniente un texto de datos en un bloque de 8 x 80 o 640 bits, de manera que se pueda transmitir una tarjeta IBM por cada bloque. De hecho, existe un sistema en operación, el Autodin, que basa la longitud de su bloque en tal criterio, siendo estos de 642 bits de largo. Los bits que exceden los 640 se usan para encabezado y verificación.

La longitud óptima del bloque es un compromiso entre la longitud del bloque y la tasa de error o la cantidad de repeticiones que se espera tener del bloque sobre un circuito particular. En los bloques largos se tiende a amortizar mejor los bits de encabezado, pero son eficientes cuando la tasa de error es alta. Bajo tales condiciones los bloques tienden a retener el circuito a causa de los periodos largos de retransmisión.

La CEA se basa en el concepto de transmisión por bloque. Cuando en el receptor se detecta un error se solicita la repetición del bloque de que se trate a la estación transmisora; la solicitud se hace a través de un canal de “retroalimentación” que puede estar dedicado especialmente a tal propósito o mediante el lado de retorno de un enlace duplex completo. En el canal de retorno dedicado, la velocidad es generalmente baja, por lo común de 75 bps, mientras que en el canal hacia adelante puede ser de 2400 bps o mayor.

Bibliografía

-Sistemas de Comunicaciones Electrónicas, Wayne Tomasi.

Páginas 512-528.

-Redes de Computadoras, Tanenbaum.

Páginas 184-190.

-Ingeniería de Sistemas de Telecomunicaciones, Freeman.

Páginas 381-391.